This post is a roughly transcribed version of my understanding of Rainer Hegselmann and Ulrich Krause’s paper, “Deliberative Exchange, Truth, and Cognitive Division of Labour: a Low-Resolution Modeling Approach”, Episteme (2009). Like all my posts, this is intended just for me, but if it is helpful for anyone else, that would make me happy 🙂
Deliberative Exchange, Truth, and Cognitive Division of Labour: a Low-Resolution Modeling Approach (2009)
Rainer Hegselmann (U. Bayreuth) and Ulrich Krause (U. Bremen)
In this paper, Hegselmann & Krause develop a formal model for the process by which individual opinions shift in a deliberative exchange with others. They intentionally take a very abstract and holistic approach, disregarding many details that I suppose they think will be filled in later.
1. Introduction
In Topics, Aristotle already works with the idea that ‘we gain knowledge through an interwoven individual and social epistemic process’. This idea is explicit in Kant & Mill: we acquire knoweldge by a process of individual reasoning and deliberative exchange with others. Social epistemology is the field studying this process.
As a field, we are looking for a well elaborated, systematic, detailed, and unified theory on how this works. In global approaches to this task, there’s nothing formal. In formal approaches, only super small questions have been addressed.
This paper wants to present a formal, global approach. For this, Hegselmann and Krause think that a low-resolution is key. Their focus for the process is on truth seeking and on the aggregation of individual opinions.
2. Low-Resolution Models of Deliberative Exchange
Let I = {1, 2, …, n} be the set of n agents in the group under consideration.
Time is an infinite sequence of periods.
Opinions are real valued numbers in the interval [0,1].
The opinion of agent i in period t is denoted as xi(t).
The profile of all opinions at time t is given by:
We want to come up with a formulation for the social process that generates for all agents i their updated opinion xi (t+1) by a deliberative exchange in period t. Hegselmann & Krause do not try to model the specifics, e.g. questions, answers, speech acts of all sorts, clarifications, inferences, weighing evidence.
They assume for each agent i a social process function fi that ‘delivers’ updated opinion xi(t+1) based on x(t), the opinion profile.
The Lehrer/Wagner-model
In Rational Consensus in Science and Society (1981) Lehrer and Wagner presented a mechanism that can be interpreted as a social process driven by iterated weighted averaging. The weights are essentially levels of credence that agents attribute to other agents. In the LW model, the social process is given by:
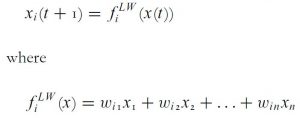
The weights are fixed nonnegative values that add to 1.
It is dynamical.
LW is not a process over time.
Starting point is dialectical equilibrium: the situation after the group engages in discussion so that all data & rationcination has occurred; further discussion would not change the opinions of any individuals in the group.
Central Question for LW: Once equilibrium is reached, is there a rational procedure to aggregate the still divergent opinions in the group? LW think yes, relying on people’s weights for expertise. But this isn’t clear.
The Bounded-Confidence-model
LW fail to address the question of how to assign weights to others. BC addresses this. They answer: “agents only take seriously, i.e. assign positive weights to, opinions that are ‘not too far away‘ from their own opinion.”
[Note to self:] This is probably accurate to the realities of cognitive operations for most people, but this is normatively problematic in my opinion / I think this is super dumb of people.
Each individual i takes into account only those individuals j for which |xi(t)−xj(t)| ≤ ε. ε is the confidence level. The set of all individuals that i takes seriously:
Individuals update opinions.
Individual i‘s opinion in the following period is set as the average of all those other individuals that i takes seriously:
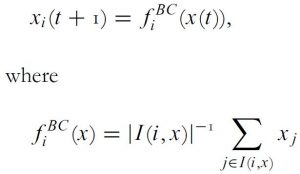
Some features of the BC model:
- Exchange processes always stabilize in finite time.
- The final pattern of opinions crucially depends on the size of ε, the confidence interval:
- small ε: plurality results.
- increased: polarization results.
- above a certain threshold: unanimity/consensus results.
- Similar to LW model, but: assigns weights
- LW: weights independent of the distance to one’s opinion, fixed over time
- BC: weights depends on the distance to one’s opinion, vary over time, like this:
- In both BC and LW: the range of opinions is preserved over time, i.e. never expands:
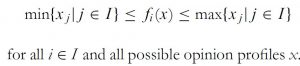
3. Modeling truth seeking agents involved in deliberative exchange
Hegselmann and Krause object to both BC and LW for the following reason: The models forget about the most decisive point of deliberative exchange: the truth. At best, they can be applied to areas only where truth does not play any role. Basically, individuals have variance on how truth-seeking they are, and this has to be accounted for in the models!
Hegselmann and Krause want to follow the KISS heuristic (“Keep it simple, stupid!” basically Occam’s razor). They take there to be a true value T somewhere in the opinion space interval [0, 1] and that T attracts at least some agents to some degree:
This represents the truth dynamics.
The opinion of i in period t + 1 is given by a convex combination with 0 ≤ αi ≤ 1.
αιT = the objective component, (1 – αi) = the social component.
αι controls the strength of the attraction of truth.
fi is the social process by LW or BC.
For α = 0, truth (T) plays no role.
H & K think their model does a good job capturing cognitive division of labor, i.e. only some individuals have an αi > 0… hahaha
Some clarifying remarks on truth dynamics equation above:
- This cannot be a mechanism intentionally followed by individuals involved, because if any given individual i understands truth and somehow knows T, then they would/should immediately update to T.
- Individuals with a positive α have access to or generate new data that point in the direction of T.
- H & K assume:
- truth is one and only one
- truth does not change over time
- truth is somewhere in the opinion space
- truth is independent of the opinions the individuals hold
- truth influences opinions
- ‘attraction of truth’: this is technical… the technical attraction of truth is used to model individuals that to a certain degree successfully aim at the truth, epistemic success based on qualities of an individual
- this does not mean that all evidence moves smoothly in T‘s direction. some evidence can point in different directions
Basically, H & K think they have created a simple formal framework for “the study of truth seeking agents embedded in a community and therein engaged in a process of deliberative exchange” (p. 135).
4. Two Analytical Results: Funnel & Leading the Pack Theorems
H & K think two theorems result from their model.
Question: Will all agents approach a consensus on the truth if they are all truth seeking (αi > 0 for all i)?
Funnel Theorem
Answer: Yes (See H & K 2006 Section 3 for proof).
Here in FT, consensus on the truth is mainly due to the objective component in the truth dynamics, but the social component can shorten the time it takes to get to said consensus.
Question: What if not all agents are truth seeking?
Leading-the-pack Theorem
For this theorem we need an understanding of what it means for agent i to be connected to agent j: For LW, given a chain of agents i1, i2,…ik:
Matrix W is irreducible if any two agents are connected. For BC, i is connected to j on time interval (s, t), for s < t and ε > ο if given a chain of agents i1, i2,…ik:
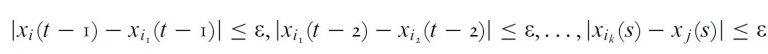
Sub-Question: What if only one single agent is truth seeking?
Answer: Yes, “consensus on the truth can be achieved even when just one single agent goes for the truth–provided all other agents are connected to this one”. Super interesting: it doesn’t matter if that truth seeking agent started off far from the truth!
For LW, consensus on the truth holds if at least one agent is going for the truth and matrix W is irreducible. If W is not irreducible, then truth seeking agent might not approach the truth, consensus can occur distinct from the truth.
For BC, consensus on the truth holds if every agent not going for the truth connects at every time interval to some other agent going for the truth, but it doesn’t have to be the same truth seeking agent. Every truth seeking agent approaches the truth (proof Kurz and Rambau 2006).
Note: the social process plays a decisive role for a consensus on the truth. Crucial: the extent to which agents are connected by chains of other agents such that each agent takes into account the opinion of the next one.
5. If not all are truth seekers: a case-study
H & K did a bunch of CASE (computer aided social epistemology) studies playing with 4 variables:
- The position of the truth T
- The frequency F of agents with α = 0
- The confidence level ε
- The strength of the truth directedness α
H & K are concerned with answering: What is the final ‘distance to the truth’ what is the final ‘truth deviation’ after the dynamics has stabilized?
They define truth deviation as:
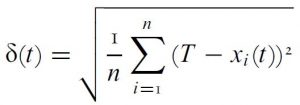
They assume a bunch of things that I am not sure they are allowed to assume:
- confidence levels ε are the same for all agents and remain constant
- a constant α
- a fixed number of 100 individuals
- a uniform start distribution
- simultaneous updating
After 1.8 million simulation runs…
Results / Conclusions:
- In all scenarios for a huge set of {α,ε} values the final truth deviation is 0.
- It does not take a whole society of truth seekers to end up with consensus on the truth, but α and ε have to have the right relation.
- For a given ε, α might be too strong, or for a given α, ε might be too small.
- “In both cases, the α-positive agents end up at the truth T, but on their way to the truth, they loose their influence on major parts of the population. The avant-garde may be ‘too good’ in the sense that for major parts of the population, the positions of the avant-garde is ‘out of range’ in a very literal sense, i.e. out of their confidence intervals. Then, what one might call a leaving-behind-effect generates a situation in which the truth seekers end up at the truth, but only among themselves, while all others live somewhere else in the opinion space, possibly polarized and quite distant from the truth.
[Note to Self:] This last bit is tragic, epistemically, and I think I should make it one of my life missions to never lose sight of this sort of effect. H & K take many assumptions for granted… if those assumptions were not set, I believe this effect would be even worse… thus, to understand the psychology, to develop the emotional intelligence and to not lose sight of being open-minded towards others’ opinions seem critical for my development.
6. Perspectives
H & K think their paper shows a framework that would allow for studying the dynamics of stylized epistemic constellations we can:
- focus on difficult situations for spreading the truth
- e.g. opinion leaders with positions distant from the truth & not interested in the truth
- e.g. asymmetric confidence intervals with a bias against the truth
- e.g. a peak far from the truth in the start
- give up the idealized assumptions on T
- e.g. evidence can be noisy
- think about truth proliferation policies
- e.g. which agents, holding which views, should have their attractions to truth modulated so that most of society can believe T?
- e.g. time pressure?
- e.g. if social exchange network structure has primarily local interactions?
- LW and BC models can be taken out and replaced for other models


